Paula - Lineare Quantenspin-Systeme

    Albert Einstein wollte nicht glauben, dass Dinge zur gleichen Zeit zwei sich ausschließende Zustände einnehmen können. Erst durch eine Messung würde das Ding gezwungen, eine der beiden Optionen einzunehmen. Welche von beiden würde aber vom Zufall entschieden.

Einsteins Zweifel lag aber eben nicht an mangelndem Verständnis für die von ihm mitbegründeten Quantenmechanik, sondern an seiner Weitsicht, die Konsequenzen aus dieser zu erkennen. Und diese müssen jedem, beim erstmaligen Aufeinanderprallen unserer sonst doch so schön klassischen Welt mit diesem Verhalten der Natur, unvorstellbar erscheinen (Sie befänden sich somit in bester Gesellschaft).

Abb. (links): Escher im Lego-Modell: Die wandelnden Mönche begegnen sich auf unmögliche Weise.

Um diese unerträgliche Tatsache zu illustrieren, betrachten Sie doch bitte die Variation eines Bildes des Künstlers Escher, auf dem zwei Kolonnen von Mönchen zu sehen sind. Die eine schreitet eine Treppe hinunter, die andere hinauf. Erst auf den zweiten Blick erkennt man, dass sich zwei einmal benachbarte Mönche nach einer Runde wieder begegnen. So als könnte man gleichzeitig hinauf und hinunter steigen. Unmöglich sagt jeder und findet nach kurzem Suchen den optischen Trick - und ist erleichtert.

In unserer Natur ist dies aber nicht unmöglich - sondern an der Tagesordnung.

Heute wissen wir aus unzähligen Experimenten, dass die Natur mit diesen Möglichkeiten spielt und beobachten hochinteressante Quantenphänomene, wie z.B. die Hochtemperatur-Supraleitung (manche Isolatoren leiten, abgekühlt auf Temperaturen die bisher sinnvoll nur im Labor erreichbar sind, Strom auf ein Mal ohne Widerstand).

Warum dies möglich ist, ist bisher nicht wirklich verstanden. Es fehlt die tiefere Einsicht, um diese Phänomene bestmöglich nutzen zu können und vielleicht in Zukunft diesen Supraleitenden Zustand bei Raumtemperatur erreichen zu können. Klassische Computer versagen kläglich bei der Simulation dieser komplexen Quanten Phänomenen aufgrund nichtüberbrückbarer, fundamentaler Schwierigkeiten.

Warum dies so ist und wie man diese scheinbar unüberwindbare Hürde nehmen könnte führt zur Thematik des Quanten-Computers/Simulators, die wir Ihnen gerne näher bringen würden.

    Viele klassische Rechenalgorithmen beinhalten so genannte "random walks", bei denen mögliche Lösungswege nach dem Zufallsprinzip ausgewählt werden. Solche Algorithmen finden in einer Reihe von Gebieten eine Anwendung, z. B. in der Physik, Biologie, in den Wirtschaftswissenschaften oder sogar in der Psychologie. Überträgt man "random walks" auf Quantensysteme, dann erübrigen sich solche Entscheidungsfindungen. Denn im Unterschied zum klassischen Verfahren liegen die in Frage kommenden Pfade in einem Superpositionszustand vor, sodass bei "Quantenwanderungen" alle gleichzeitig beschritten werden können. Die dabei auftretenden Interferenzen führen zu neuartigen Phänomenen- so kann der "Quantenwanderer" sich z. B. an manchen Kreuzungen selbst begegnen. "Quantum walks" könnten zum einen Rechenalgorithmen für Quantensysteme erheblich beschleunigen. Sie könnten aber auch dazu beitragen, den an mesoskopischen Systemen zu Tage tretenden Grenzbereich zwischen der klassischen und der quantenmechanischen Welt besser zu begreifen. Mit einem "proof-of-principle experiment" in einer elektromagnetischen Falle haben jetzt Dr. Tobias Schätz, Leiter der Arbeitsgruppe "Atom-, Molekül- und optische Physik" des Physikalischen Insituts der Universität Freiburg, und seine Mitarbeiter erstmals deutlich den Unterschied zwischen der klassischen und der quantenmechanischen "Odyssee" - mit einem Ion als Wanderer [Phys. Rev. Lett. 103, 090504 (2009)].

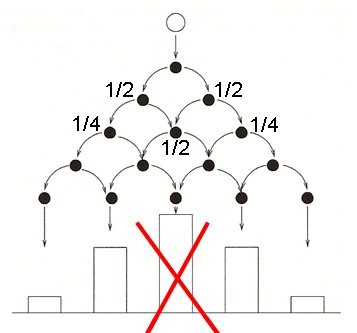Abb. (links): Galton's Board, "Klassische" Murmeln fallen durch ein Nagelbrett. Die Nägel sind in Reihen angeordnet und haben alle den selben Abstand zueinander. Wenn eine Murmel einen dieser Nägel trifft, fällt sie mit der gleichen Wahrscheinlichkeit nach links oder rechts. Unter der letzten Reihe befinden sich eine Reihe von Bechern, die die Murmeln auffangen. Die Verteilung, die sich ergibt, ist eine Gaußglocke (alter 10-DM-Schein). Interferenzeffekte einer "Quanten-Murmel" können dazu führen, dass einzelne Becher leer bleiben.

Jedes Mal, wenn wir an eine Kreuzung kommen, müssen wir uns - vielleicht per Münzwurf - zwischen mehreren Wegen entscheiden. Nach mehreren Kreuzungen und Entscheidungen werden wir nur einige von vielen möglichen Pfaden gegangen sein. Dabei kann es vorkommen, dass manche Wege häufiger als andere beschritten werden.

Im Gegensatz dazu braucht sich ein "Quantenwanderer" nicht zu entscheiden, denn er hat gar keine Wahl. Bei jedem Münzwurf wird vielmehr eine Superposition von Kopf und Zahl erzeugt, sodass er allen Pfaden gleichzeitig folgen kann. Dabei kann es zu sonderbaren Situationen kommen, z. B. kann der Quantenwanderer, wenn Pfade an späteren Kreuzungen wieder aufeinander stoßen, sich selbst begegnen. Aufgrund von Interferenzeffekten kann sich die Wahrscheinlichkeit dafür, an dieser Kreuzung zu sein, erhöhen, aber auch soweit verringern, dass er von dort gänzlich verschwindet.

In dem hier beschriebenen Experiment spielt ein einzelnes Magnesium-Ion, das in einer linearen elektromagnetischen Falle festgehalten wird, die Rolle des Quantenwanderers. Sein Bewegungsgrundzustand ist sozusagen die Ausgangsposition, von der aus es los marschiert. Durch Einstrahlung von Radiofrequenz-Pulsen wird eine Überlagerung von zwei elektronischen Zuständen angeregt. Dieser Vorgang entspricht dem Münzwurf, durch den man eine Superposition von "linker" und "rechter" Wegentscheidung (Kopf und Zahl) erhält. Den notwendigen "Schubs", sich in Bewegung zu setzen, erhält das Ion durch ultraviolettes Licht einer genau abgestimmten Frequenz. Abhängig von seinem elektronischen Zustand wird das Ion von dem UV-Licht mal nach links und mal nach rechts gestoßen. Da die beiden elektronischen Zustände - Kopf und Zahl - in einem Überlagerungszustand vorliegen, werden auch die beiden Bewegungsmöglichkeiten des Ions - Schritt nach rechts und/oder Schritte nach links - überlagert. Bei der Quantenwanderung sind daher die beiden Münzwerte mit den beiden Bewegungsmöglichkeiten des Ions hochgradig verschränkt.

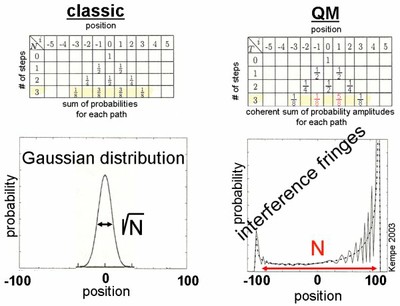
Abb. (oben): Das Pascal'sche Dreieck und die zugehörige Wahrscheinlichkeitsverteilung (nach 100 Schritten, nur die geradzahligen sind Werte sind ungleich null und gezeichnet) einer klassischen Irrfahrt (random walk, links) und einer Quanten-Irrfahrt (quantum walk, rechts): Die Wahrscheinlichkeit, sich nach N Schritten an Position i wiederzufinden. Die quantenmechanische Variante weicht ab dem dritten Schritt vom klassischen Pendant ab. Die symmetrische klassische Wahrscheinlichkeitsverteilung ist um die Position 0 herum am stärksten konzentriert. Die Breite wächst Proportional zur Wurzel der Anzahl der Schritte. Die Wahrscheinlichkeitsverteilung des quantenmechanischen Laufs (Berechnung) zeigt ein komplexes Interferenzmuster, das zu einer Ausdünnung der inneren und zu einer Verstärkung der Wahrscheinlichkeiten für die äußeren Positionen führt, in unserem Fall werden die rechten Positionen auf Grund der Interferenz bevorzugt. Die Breite wächst quadratisch schneller als im klassischen Fall.

Die Vorgänge "Münzwurf" und "Positionswechsel" werden insgesamt drei Mal wiederholt, erst dann können Quanteneffekte sichtbar werden. Nach Beendigung dieser "Quantenevolution" wird gemessen, ob die Münze Kopf oder Zahl zeigt und auf welcher Position sich das Ion befindet. Dabei wird ausgenutzt, dass das Ion nur in einem der beiden "Münzzustände" Fluoreszenzlicht aussendet. Nach etwa tausend Messungen erhalten die Physiker so eine statistische Aussage darüber, wie häufig das Ion nach "rechts" oder "links" gegangen ist. Ihre Messdaten bestätigen die theoretische Vorhersage eines Ungleichgewichts beider Richtungen, im Gegensatz zu dem, was man von einem klassischen System erwarten würde.

Die Gruppe von Tobias Schätz hat mit diesem Experiment, bei dem der Wanderer/das Ion alle Wege gleichzeitig gehen darf, deutlich die Unterschiede zum klassischen Gegenstück aufgedeckt: Die Quanteninterferenz verstärkt asymmetrische, nicht-klassische Verteilungen in den miteinander hochverschränkten Münzwurf- und Bewegungszuständen. Derzeit ist die Zahl der Wiederholungsschritte noch durch nichtlineare Effekte begrenzt. Die Wissenschaftler schlagen ein neues Konzept vor, mit dem sich die Quantenwanderung auf viele, im Prinzip sogar mehrere hundert Schritte ausdehnen lässt.

"Quantenwanderungen" könnten für eine Reihe von Anwendungen von fundamentalem Interesse sein. So lässt sich die Geschwindigkeit, den richtigen Weg zu finden, unter Umständen gewaltig steigern, wenn man nicht nach dem Zufallsprinzip einen nach dem anderen ausprobieren muss, sondern gleichzeitig alle beschreiten kann. Die Leistungsfähigkeit von Suchalgorithmen in der Informationsverarbeitung könnte dadurch erheblich gesteigert werden. Es gibt des weiteren Überlegungen, dass dieses quantenmechanische Verhalten auch für den Energietransfer in Pflanzen verantwortlich ist, der auf viele Wege verteilt weit effektiver verläuft, als mit klassischen Verfahren erreichbar wäre.

Ein schöner Übersichtsartikel in Englisch findet sich hier: Kempe, Quantum random walks - an introductory overview